Geo Progression Formula
Common ratio = r = T n / T n1.

Geo progression formula. Math Formulas Arithmetic and Geometric Series Notation Number of terms in the series n First term a 1 Nth term a n Sum of the rst n terms S n Di erence between successive terms d Common ratio q Sum to in nity S Arithmetic Series Formulas 1 a n = a 1 (n 1)d 2 a i = a i 1 a i1 2 3 S n = a 1 a n 2 n 4 S n = 2a 1 (n 1)d 2 n. The general formula for the geometric mean of n numbers is the nth root of their product For example = GEOMEAN (4, 9) // returns 6 The longhand calculation would be = (4 * 9) ^ (1 / 2) = (36) ^ (1 / 2) = 6 The arithmetic mean would be (4 9)/2 = 65 In the example shown, GEOMEAN is used to calculate a compound annual growth rate To to. When three quantities are in GP, the middle one is called as the geometric mean of the other two If a, b and c are three quantities in GP and b is the geometric mean of a and c ie The sum of infinite GP series.
Aarar 2 ar 3 and so on Geometric progression represents the growth of geometric shapes by the fixed ratio, hence the dimension in the sequence matters Only whole numbers can be used in a geometric progression. S_n =( a(1r^n))/(1r) Now given you know r n and the sum you find a by re arranging Additionally If you re given the nth term then' a_n = ar^(n1) You may often has to use both these equation to get to the answer. This geometric sequence has a common ratio of 3, meaning that we multiply each term by 3 in order to get the next term in the sequence The recursive formula for a geometric sequence is written in the form For our particular sequence, since the common ratio (r) is 3, we would write.
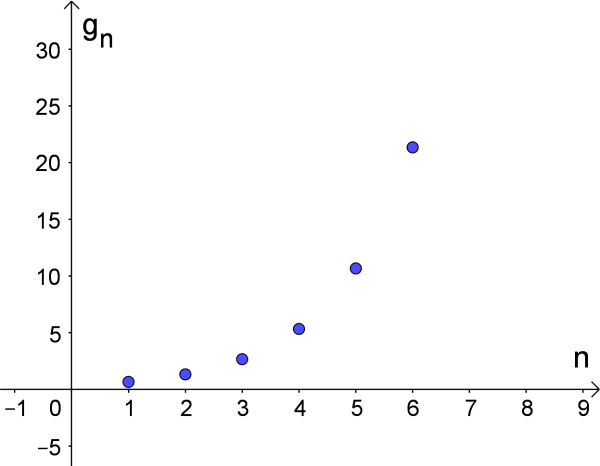
An = a1rn−1 a n = a 1 r n − 1 Let’s take a look at the sequence {18, 36, 72, 144, 2, } { 18 , 36 , 72 , 144 , 2 , } This is a geometric sequence with a common ratio of 2 and an exponential function with a base of 2 An explicit formula for this sequence is an =18 ⋅2n−1 a n = 18 ⋅ 2 n − 1. Find The Formula For A Geometric Sequence Given Terms This video explains how to find the formula for the nth term of a given geometric sequence given three terms of the sequence Example Given the information about the geometric sequence, determine the formula for the nth term a 0 = 5, a 1 = 40/9, a 3 = 3/81, Show Video Lesson. The GP series formula applied to calculate the sum of geometric progression of first n terms of a GP and ;.
Finite Geometric Series To find the sum of a finite geometric series, use the formula, S n = a 1 ( 1 − r n) 1 − r, r ≠ 1 , where n is the number of terms, a 1 is the first term and r is the common ratio Example 3 Find the sum of the first 8 terms of the geometric series if a 1 = 1 and r = 2 S 8 = 1 ( 1 − 2 8) 1 − 2 = 255. Example of Geometric Mean If you have $10,000 and get paid 10% interest on that $10,000 every year for 25 years, the amount of interest is $1,000 every year for 25 years, or $25,000. Geometric progression In geometric progression, a1 = 7, q = 5 Find the condition for n to sum first n members is sn≤217 Geometric progression 2 There is geometric sequence with a 1 =57 and quotient q=25 Calculate a 17 Geometric seq Find the third member of geometric progression if a1 a2 = 36 and a1 a3 = 90 Calculate its quotient.
Geometric Progression, Series & Sums Introduction A geometric sequence is a sequence such that any element after the first is obtained by multiplying the preceding element by a constant called the common ratio which is denoted by r The common ratio (r) is obtained by dividing any term by the preceding term, ie,. Formula is Tn=a*(r^(n1)) a=3/16 Tn=96 r=2 I have to find this n with this formula, but I don't know how Please Help me !!. The General Term of Geometric Progression The n th term of Arithmetic Progression was found out to be x n = x (n 1) b In the case of Geometric Progression, let’s assume that x is the first number and “r” is the common ratio between all the numbers So, the second term would be x 2 = x * r The third term would be x 3 = x 2 * r = x.
Free Geometric Sequences calculator Find indices, sums and common ratio of a geometric sequence stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie Policy. Geometric progression is a sequence of numbers where each term after the first is found by multiplying the previous one by a fixed nonzero number called the common ratio If the common ratio module is greater than 1, progression shows the exponential growth of terms towards infinity;. Since arithmetic and geometric sequences are so nice and regular, they have formulas For arithmetic sequences, the common difference is d, and the first term a1 is often referred to simply as "a" Since we get the next term by adding the common difference, the value of a2 is just a2 = a d.
If time allows, review the formula for finding the nth term in a geometric sequence and apply the formula to two more realworld examples Exit Ticket (10 minutes) Next, allow students time to review what they learned during the lesson and explain their understanding in their own words with diagrams, examples, and words. Identify the Sequence, , This is a geometric sequence since there is a common ratio between each term In this case, multiplying the previous term in the sequence by gives the next term In other words, Geometric Sequence This is the form of a geometric sequence Substitute in the values of and. For example, the sequence 2, 10, 50, 250, 1250, 6250, , , is a geometric progression with the common ratio being 5 The formulas applied by this geometric sequence calculator are detailed below while the following conventions are assumed the first number of the geometric progression is a;.
That is, a n =r⋅a (n1) for every n>1 A sequence is geometric if each term can be obtained from the previous one by multiplying by the same nonzero constant A geometric sequence is also referred to as a geometric progression For example 2, 10, 50, 250, is a geometric sequence as each term can be obtained by multiplying the previous term by 5. Geometric Progression Formulas The list of formulas related to GP are given below which will help in solving different types of problems The general form of terms of a GP is a, ar, ar 2, ar 3, and so on Here, a is the first term and r is the common ratio The nth term of a GP is T n = ar n1;. To find the sum of the first S n terms of a geometric sequence use the formula S n = a 1 (1 − r n) 1 − r, r ≠ 1, where n is the number of terms, a 1 is the first term and r is the common ratio The sum of the first n terms of a geometric sequence is called geometric series.
Identify the ratio of the geometric sequence and find the sum of the first eight terms of the sequence 5, 15, 45, 135, 405, 2 A ball is dropped from a height of 10 feet. Given the first term and the common ratio of a geometric sequence find the first five terms and the explicit formula 15) a 1 = 08 , r = −5 16) a 1 = 1, r = 2 Given the first term and the common ratio of a geometric sequence find the recursive formula and the three terms in the sequence after the last one given 17) a 1 = −4, r = 6 18) a 1. If it is less than 1, but not zero, progression shows exponential decay of terms towards zero.
Guidelines to use the calculator If you select a n, n is the nth term of the sequence If you select S n, n is the first n term of the sequence For more information on how to find the common difference or sum, see this lesson Geometric sequence. Geometric Mean Formula The formula to calculate the geometric mean is given below The Geometric Mean (GM) of a series containing n observations is the nth root of the product of the values Consider, if x 1, x 2 X n are the observation, then the GM is defined as. The terms of a geometric series are also the terms of a generalized Fibonacci sequence (F n = F n1 F n2 but without requiring F 0 = 0 and F 1 = 1) when a geometric series common ratio r satisfies the constraint 1 r = r 2, which according to the quadratic formula is when the common ratio r equals the golden ratio (ie, common ratio r = (1.
Geometric Progression often abbreviated as GP in mathematics, is a basic mathemetic function represents the series of numbers or n numbers that having a common ratio between consecutive terms For example, 2, 4, 8, 16 n is a geometric progression series that represents a, ar, ar 2, ar 3 ar (n1);. In this minilesson, we will explore the world of arithmetic progression and geometric progression in math You will get to learn about the arithmetic progression formula, geometric progression formula, sum of arithmetic progression, geometric progression sum, and other interesting facts around the topic. First, we will develop a formula for this sequence using the explicit rule The first term, a 1, is 1 and the common ratio is 2 a n = (a 1)r n1 a n = (1)(2) n1 a n = 2 n1 We know the last number in the sequence This last number, 256, is a n Using the formula, we get this.
Where 2 is a first term a, the common ratio r is 3 and the total number of terms n is 10. Geometric Progression Definition A geometric progression is a sequence in which any element after the first is obtained by multiplying the preceding element by a constant called the common ratio which is denoted by r For example, the sequence 1, 2, 4, 8, 16, 32 is a geometric sequence with a common ratio of r = 2 Here the succeeding number in the series is the double of its preceding number. The geometric progression can be written as ar 0 =a, ar 1 =ar, ar 2 , ar 3 , where r ≠ 0 , r is the common ratio and a is a scale factor(also the first term).
In geometric sequences there is a case of repeated multiplication Look down for more a,ar,ar^2,ar^(n1 n So the sum of the first n terms of sequence is ;. The desired result, 312, is found by subtracting these two terms and dividing by 1 − 5 A geometric series is the sum of the numbers in a geometric progression For example 2 10 50 250 = 2 2 × 5 2 × 5 2 2 × 5 3 {\displaystyle =22\times 52\times 5^ {2}2\times 5^ {3}}. How to prove the formula for the sum of the first n terms of a geometric series, using an algebraic trick Also, agrief look at an alternative method.
Geometric series is a sequence of terms in which next term is obtained by multiplying common ration to previous term The (n1) th term of GP can be calculated as (n1) th = n th x R where R is the common ratio (n1) th /n th The formula to calculate N th term of GP t n = a x r n1 where, a is first term of GP and r is the common ratio C program to print geometric progression series and it. Geometric Sequence Formulas 1 Terms Formula a n = a 1 (r n1) 2 Sum Formula S n = a 1 (1 r n) / (1 r) Where a n is the nth term of the sequence, a 1 is the first term of the sequence, n is the number of terms, r is the common ratio, S n is the sum of the first n terms of the sequence. In geometric sequences there is a case of repeated multiplication Look down for more a,ar,ar^2,ar^(n1 n So the sum of the first n terms of sequence is ;.
A = 10 (the first term) r = 3 (the "common ratio") The Rule for any term is xn = 10 × 3(n1) So, the 4th term is x 4 = 10 × 3 (41) = 10 × 3 3 = 10 × 27 = 270 And the 10th term is x 10 = 10 × 3 (101) = 10 × 3 9 = 10 × 196 = 1960 A Geometric Sequence can also have smaller and smaller values. A geometric sequence is a sequence derived by multiplying the last term by a constant Geometric progressions have many uses in today's society, such as calculating interest on money in a bank account So if you were wondering how exactly you would work out how much money you'll have in there in a few years, this article will help you find out. A geometric sequence is a special progression, or a special sequence, of numbers, where each successive number is a fixed multiple of the number before it Let me explain what I'm saying So let's say my first number is 2 and then I multiply 2 by the number 3.
A geometric sequence refers to a sequence wherein each of the numbers is the previous number multiplied by a constant value or the common ratio Let’s have an example to illustrate this more clearly For instance, you’re growing root crops Let’s assume that for each root crop you plant, you get root crops during the time of harvest. An arithmeticgeometric progression (AGP) is a progression in which each term can be represented as the product of the terms of an arithmetic progressions (AP) and a geometric progressions (GP) In the following series, the numerators are in AP and the denominators are in GP. Is called a geometric sequence, or geometric progression, if there exists a nonzero constant r, called the common ratio, such that That is, an = r ⋅ a(n1) for every n >1 A sequence is geometric if each term can be obtained from the previous one by multiplying by the same nonzero constant.
Geometric Progression, GP Geometric progression (also known as geometric sequence) is a sequence of numbers where the ratio of any two adjacent terms is constant The constant ratio is called the common ratio, r of geometric progression Each term therefore in geometric progression is found by multiplying the previous one by r Eaxamples of GP 3, 6, 12, 24, is a geometric. S_n =( a(1r^n))/(1r) Now given you know r n and the sum you find a by re arranging Additionally If you re given the nth term then' a_n = ar^(n1) You may often has to use both these equation to get to the answer. S n= 1575, r= 05, a n= 025 S n= 244, r= –3, n= 5 Use Formula 3 S n= 1575, r= 05, a n= 025 Use Formula 4 Formula 5 If a geometric series is infinite (that is, endless) and –1 < r< 1, then the formula for its sum becomes If r> 1 or if r< –1, then the infinite series does not have a sum Example 4.
R = common ratio of geometric progression S = sum of the 1 st n terms Arithmetic Progression, AP Arithmetic progression is a sequence of numbers in which the difference of any two adjacent terms is constant The constant difference is commonly known as common difference and is denoted by d Examples of arithmetic progression are as follows. Geometric Progression (GP) Harmonic Progression (HP) A progression is a special type of sequence for which it is possible to obtain a formula for the nth term The Arithmetic Progression is the most commonly used sequence in maths with easy to understand formulas Let’s have a look at its three different types of definitions. This algebra video tutorial provides a basic introduction into geometric series and geometric sequences It explains how to calculate the common ratio of a.
So this is a geometric series with common ratio r = –2 (I can also tell that this must be a geometric series because of the form given for each term as the index increases, each term will be multiplied by an additional factor of –2) The first term of the sequence is a = –6Plugging into the summation formula, I get. The step/common ratio is r;. R = common ratio of geometric progression S = sum of the 1 st n terms Arithmetic Progression, AP Arithmetic progression is a sequence of numbers in which the difference of any two adjacent terms is constant The constant difference is commonly known as common difference and is denoted by d Examples of arithmetic progression are as follows.
Geometric series is a sequence of terms in which next term is obtained by multiplying common ration to previous term The (n1) th term of GP can be calculated as (n1) th = n th x R where R is the common ratio (n1) th /n th The formula to calculate N th term of GP t n = a x r n1 where, a is first term of GP and r is the common ratio C program to print geometric progression series and it. Given the first term and the common ratio of a geometric sequence find the first five terms and the explicit formula 15) a 1 = 08 , r = −5 16) a 1 = 1, r = 2 Given the first term and the common ratio of a geometric sequence find the recursive formula and the three terms in the sequence after the last one given 17) a 1 = −4, r = 6 18) a 1. N^ {\text {th}} nth term of the AGP is obtained by multiplying the corresponding terms of the arithmetic progression (AP) and the geometric progression (GP) So, in the above sequence the t n = a ( n − 1) d r n − 1 = a(n−1)drn−1 S n = a − a ( n − 1) d r n 1 − r d r ( 1 − r n − 1) ( 1 − r) 2.
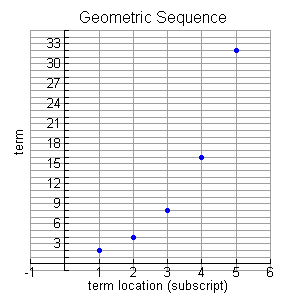
Geometric Progression Formula and Example In mathematics, Geometric Progression (GP) is a sequence of numbers where any element after the first is obtained by multiplying the preceding element by a constant called the common ratio Here is a simple tutorial which helps you to learn how to calculate Geometric Progression (GP). A sequence, on the other hand, is a set of numbers such as 2,1,3 where the order of the numbers is important A different sequence from the above is (compound interest) applications of the geometric progression, the formula is written assuming that r is less than one, but if r is greater than 1, then the minuses cancel out Bonus If n is. The graph plotted for a geometric sequence is discrete Mathematically, a geometric sequence can be represented in the following way;.
And so this is our formula for the sum of an infinite geometric sequence So let's do an example finding the sum of an infinite geometric sequence using our formula So I've got an infinite geometric sequence here, 11, 55, 275, 1375, et cetera We need to use our formula to find the sum So I'll have S is equal to a1. Arithmetic progression and geometric progression formulas On the webpage, we can find the formulas used in the topic arithmetic and geometric progression General form of arithmetic progression a , (ad), (a2d), (a3d), nth term or general term of the arithmetic sequence an = a(n1)d here "n" stands for the required term. Divide each term by the previous term to determine whether a common ratio exists 2 1 = 2 4 2 = 2 8 4 = 2 16 8 = 2 2 1 = 2 4 2 = 2 8 4 = 2 16 8 = 2 The sequence is geometric because there is a common ratio The common ratio is 2 12 48 = 1 4 4 12 = 1 3 2 4 = 1 2 12 48 = 1 4 4 12 = 1 3 2 4 = 1 2.
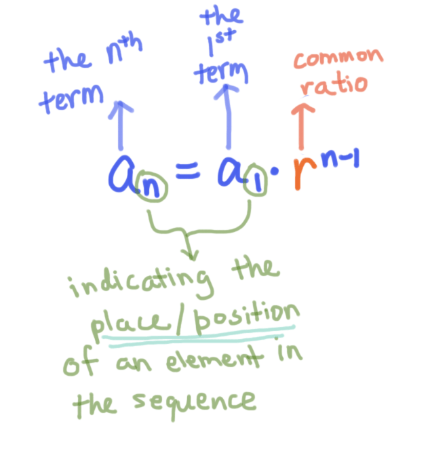
This is a geometric sequence since there is a common ratio between each term In this case, multiplying the previous term in the sequence by 3 3 gives the next term In other words, an = a1rn−1 a n = a 1 r n 1 Geometric Sequence r = 3 r = 3. In short, a sequence is a list of items/objects which have been arranged in a sequential way A series can be highly generalized as the sum of all the terms in a sequence However, there has to be a definite relationship between all the terms of the sequence The fundamentals could be better understood by solving problems based on the formulas. What we saw was the specific explicit formula for that example, but you can write a formula that is valid for any geometric progression you can substitute the values of a₁ for the corresponding initial term and r for the ratio The general formula for the nth term is aₙ = a₁ * rⁿ⁻¹ n ∈ 𝗡,.
Geometric Progression is a sequence like 1, ½ , ¼ in which the ratio of a term to its predecessor is always same The advanced online Geometric Progression Calculator is used to calculate the progression of the given nth term, first term and the common difference. Geometric progression or sequence, is a sequence of numbers where each term after the first is found by multiplying the previous one by a fixed nonzero number called the common ratio For example, the series 2, 6, 18, 54,.

Arithmetic And Geometric Series And Summation Formulas Geogebra

Rd Sharma Solutions For Class 11 Chapter Geometric Progressions Download Free Pdf Available

Geometric Progression Formula
Geo Progression Formula のギャラリー

Proof For The Geometric Series Formula Youtube

Using Recursive Formulas Of Geometric Sequences Video Khan Academy
Geometric Sequences And Series Mathbitsnotebook Ccss Math

Sn For Geometry Progression Gp Youtube

1 5 1 Geometric Progressions Spm Practice Paper 1 Spm Additional Mathematics

1 4 3 Sum Of The First N Terms Of A Geometric Progression Spm Additional Mathematics

Geometric Progression Formulas And Properties Sum Of Geometric Series

Geometric Progressions
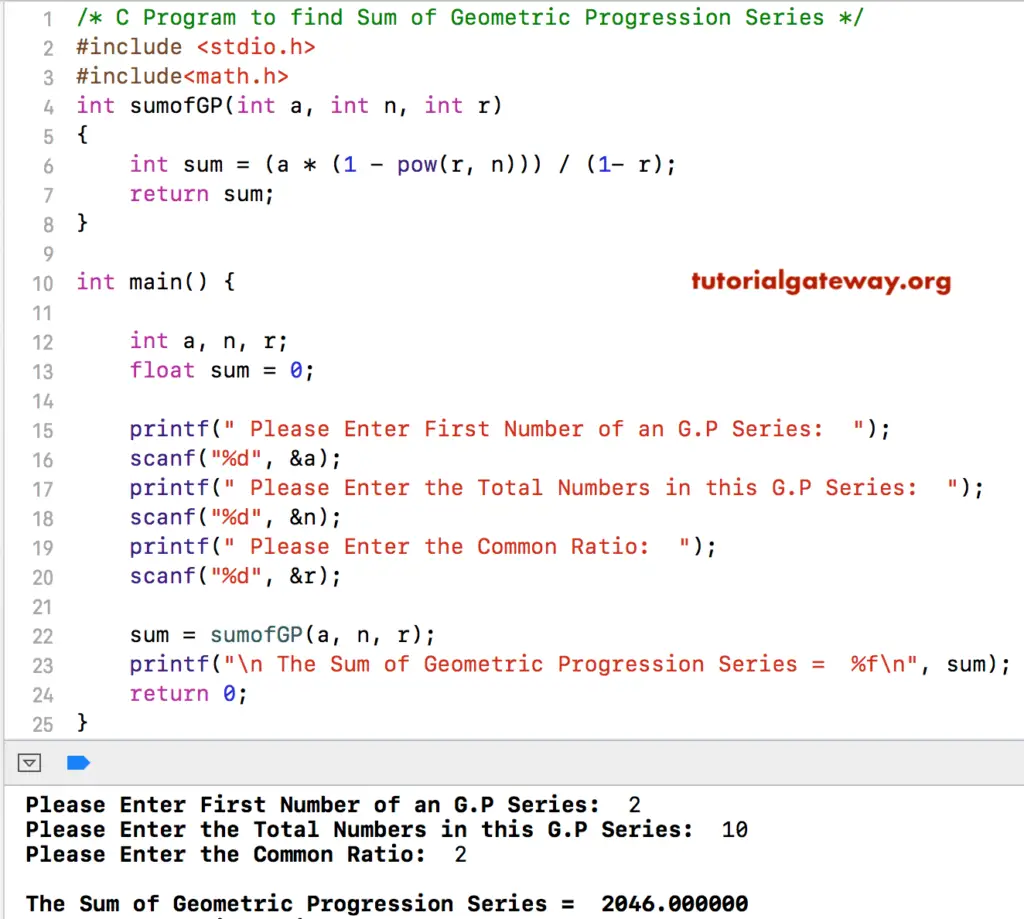
C Program To Find Sum Of Geometric Progression Series

Geometric Progression Series And Sums An Introduction To Solving Common Geometric Series Problems

Geometric Sequence Calculator Symbolab
2 2 Arithmetic And Geometric Sequences Mathematics Libretexts

Geometric Progression Formula Assignment Point

How To Proceed Further In This Arithmetico Geometric Progression Problem Mathematics Stack Exchange

Nth Term Of A Geometric Sequence Mr Mathematics Com

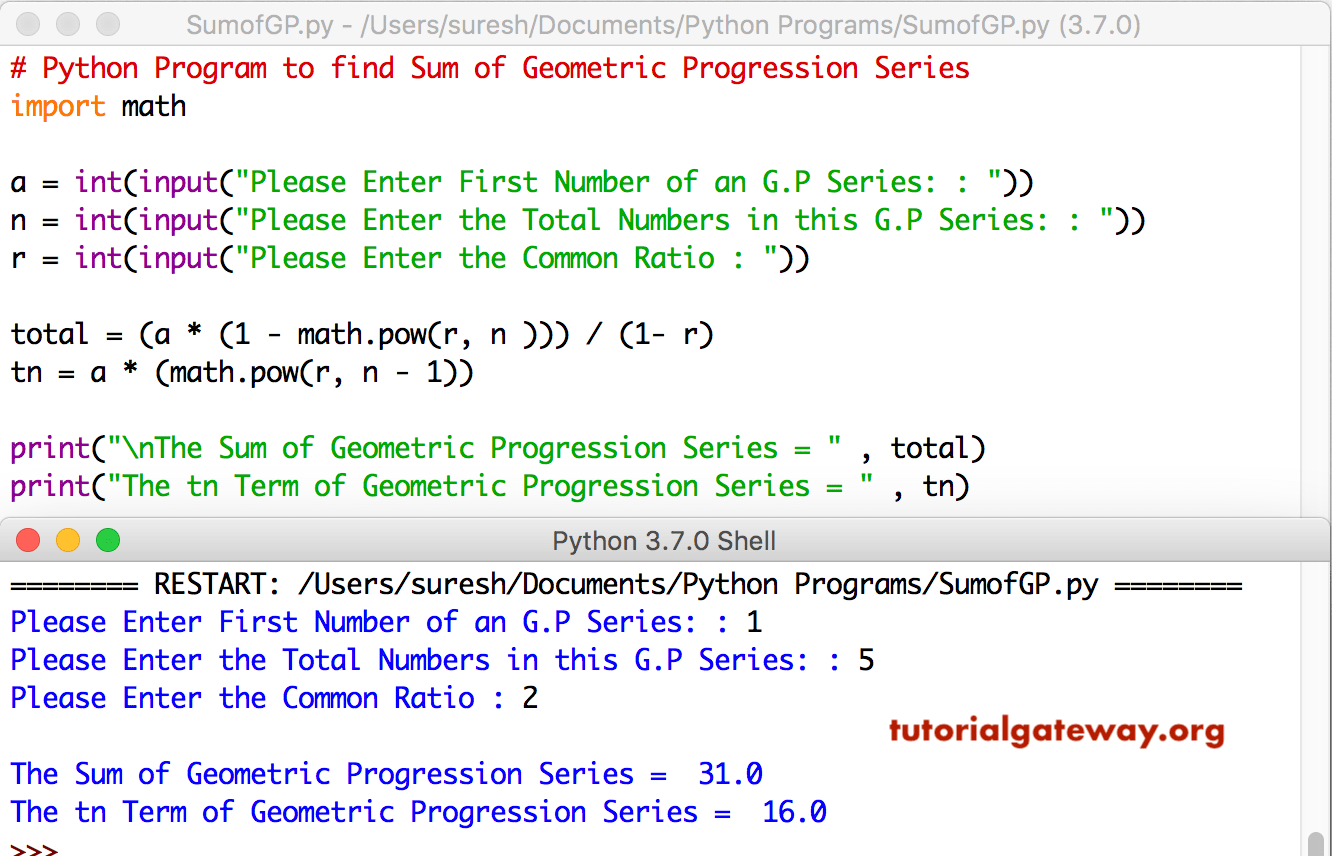
Python Program To Find Sum Of Geometric Progression Series

Geometric Progression Geeksforgeeks

Geometric Sequences And Sums

Geometric Progression Series And Sums An Introduction To Solving Common Geometric Series Problems

Quiz Worksheet Geometric Sequences Study Com
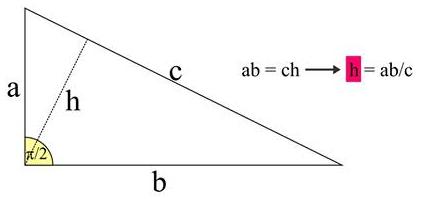
Pythagorean Theorem Via Geometric Progression

Geometric Series Applications Examples Solutions Videos Worksheets Activities

Geometric Progression Series And Sums An Introduction To Solving Common Geometric Series Problems

How To Solve Geometric Mean And Progression
Python Program To Find Sum Of Geometric Progression Series

Compound Interest And Geometric Progression

Vocabulary And Formulas For Sequences

Geometric Series Proof Of The Formula For The Sum Of The First N Terms Youtube

Arithmetic And Geometric Sequence Sum Nth Term Cheat Sheet Foldable Arithmetic Sequences Geometric Sequences Maths Solutions

Understand The Formula For Infinite Geometric Series Video Lesson Transcript Study Com

Recursive Formulas For Geometric Sequences Practice Khan Academy

Arithmetic And Geometric Series Progressions

Geometric Sequences And Series Boundless Algebra
Geometric Progression Wikipedia
Geometric Progression Solver N Th Value Sum Calculator

Geometric Series Formula Concepts Videos And Practice Questions

Geometric Progression Geeksforgeeks

Arithmetic And Geometric Sequences And Series Chart Sequence And Series Geometric Sequences Arithmetic Sequences

Geometric Sequence Calculator

How To Find Any Term Of A Geometric Sequence 4 Steps

Arithmetic Progression Geometric Progression And Analytical Geometry Math Formulas Arithmetic Progression Math

Compound Interest And Geometric Progression

Geometric Progression Study Material For Iit Jee Askiitians
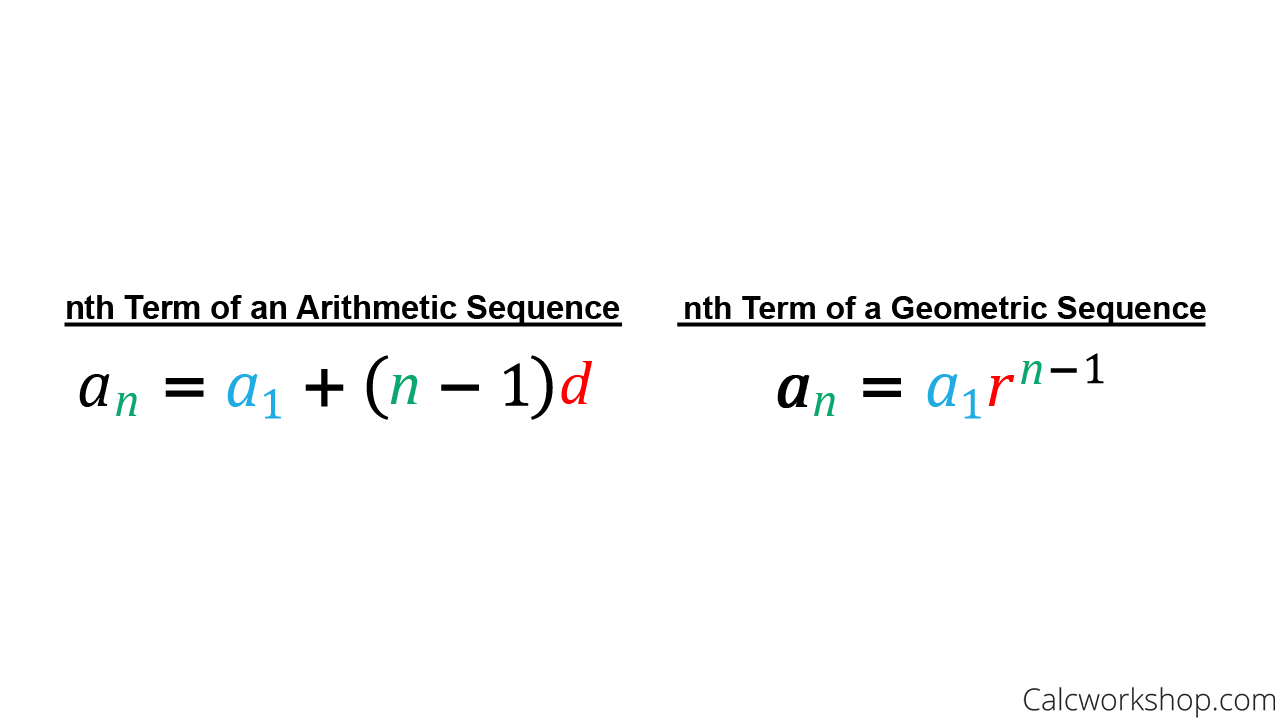
Arithmetic And Geometric Sequences 17 Amazing Examples

Mathematical Formula Geometric Progression Teaching Poster Stock Vector Royalty Free
Recursive And Explicit Formulas For Geometric Sequences Expii

Sum Of An Infinite Gp Solved Examples Algebra Cuemath

Maths Group5 Geometric Progression Formula
Q Tbn And9gcregxqobsjmoo5jqn9 Phdhf7xhnadnswikj4jpetarhlgln7ao Usqp Cau
Http Www Angelfire Com Alt M9233 03apgp Lwh Ok Pdf
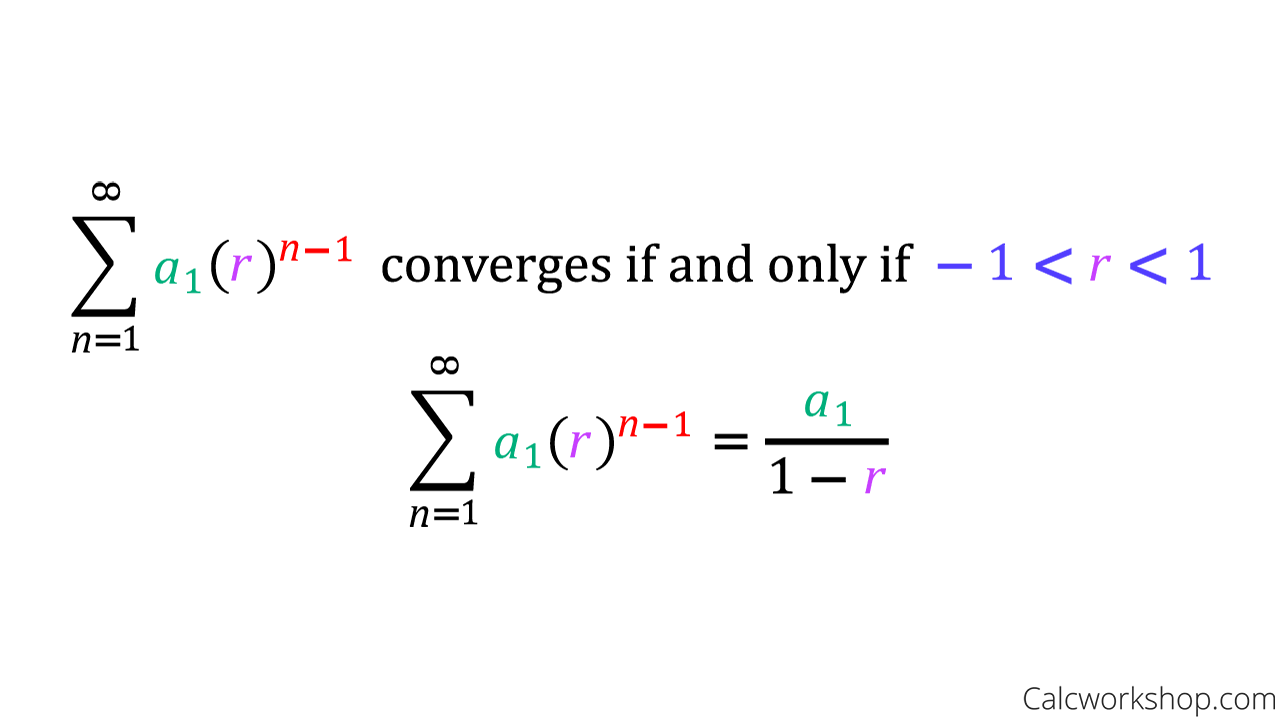
Geometric Series

Derivation Of General Term Sum Of Finite And Infinite Geometric Progression M Cube Mathematics By Maheshwari

Topic 2 Sum Of Geometric Series And Constant Dividend Growth Model Studocu
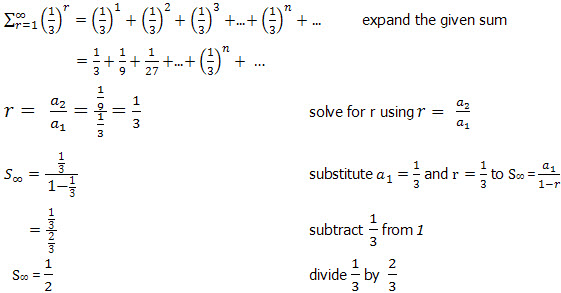
Geometric Progression Series And Sums An Introduction To Solving Common Geometric Series Problems

Geometric Sequence Formula Examples Video Lesson Transcript Study Com

Geometric Progressions Math Formulas Mathematics Formulas Basic Math Formulas

How Is The Sum Of Infinite Geometric Progression Derived Does Arithmetic Progression Also Have Formulae For The Sum Of Infinite Aps Quora

Geometric Sequences And Series Further Maths U3 4

Geometric Progression Formula Concepts Tricks Solved Problems Face Prep
Geometric Progression Wikipedia
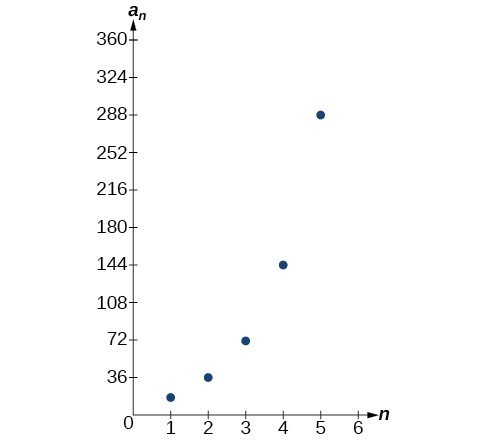
Explicit Formulas For Geometric Sequences College Algebra

Geometric Sequences And Series Examples Solutions Videos

Cbse Class 11 Maths Notes Sequences Series Geometric Progression Aglasem Schools

1 4 3 Sum Of The First N Terms Of A Geometric Progression Spm Additional Mathematics

Geometric Sequence Advanced Higher Maths

Geometric Series Wikipedia

Arithmetic And Geometric Sequences And Series Chart Sequence And Series Formula Chart Geometric Sequences

Geometric And Arithmetic Progression Hitbullseye
Q Tbn And9gcrvvot2b6ws1wp0ftjgh70qse7kfjvcxeasm X8ywowcnsracvh Usqp Cau

Geometric Sequences Nth Term Video Lessons Examples And Solutions
Miraculous World Of Numbers 56 06 Basics Of Arithmetic Geometric Progression Grades 9 To 12 Part 06
Past Paper Items On Arithmetic And Geometric Sequences And Series Cie Math Solutions

Solved I Let Be A Geometric Progression With G E And Chegg Com
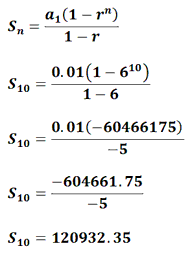
Geometric Sequences And Series

Deriving The Sum Of The Geometric Sequence

Geometric Progression Assignment Point

Geometric Progression Wikipedia

Geometric Series Examples Solutions Videos Worksheets Games Activities
Sequences And Series A Level Maths Uptuition With Mr Will

Ixl Write A Formula For A Geometric Sequence Algebra 2 Practice

Finding And Classifying Geometric Sequences Video Lesson Transcript Study Com
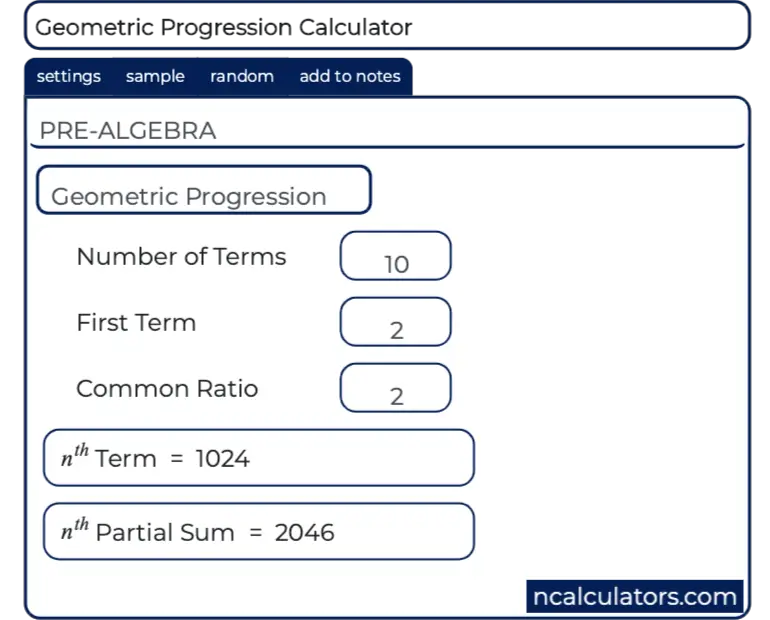
Geometric Progression Solver N Th Value Sum Calculator

Geometric Sequences And Series Further Maths U3 4
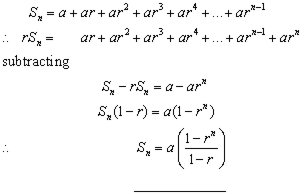
Geometric Series Progression Series Sequences Pure Mathematics From A Level Maths Tutor

Geometric Sequences And Series Further Maths U3 4

Geometric Progression Series And Sums An Introduction To Solving Common Geometric Series Problems

Compound Interest And Geometric Progression

Geometric Progression Gp Calculator

Geometric Progression Definition Formulas Properties And Examples
11 Sequences Series Financial Mathematics Mathscafe Net

Arithmetico Geometric Sequence Wikipedia
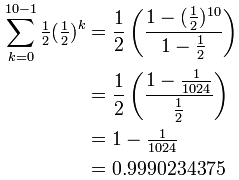
Geometric Sequences And Sums

Recursive And Explicit Formulas For Geometric Sequences Expii
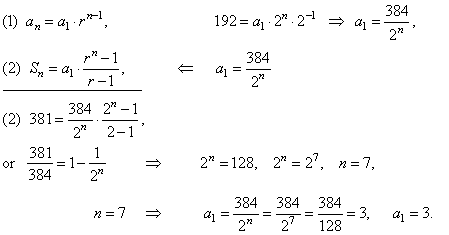
Sequences And Series Geometric Sequence Or Progression
Q Tbn And9gctqhya5anpkzpwtcbe9mhhzrbqlj3ssjwwrvzdnnljhaymw1gly Usqp Cau

Geometric Progression An Overview Sciencedirect Topics

What Is Arithmetico Geometric Sequence A Plus Topper

Solved Please Help Having Difficulty With Precalc The To Chegg Com

Proof Of The Pythagorean Theorem Based On Geometric Progression Formula By John Arioni Mathematics Geometry Pythagorean Theorem Math Methods

Using Explicit Formulas Of Geometric Sequences Video Khan Academy



