Geo Sequence Formula
The sequences of numbers are following some rules and patterns This pattern may be of multiplying a fixed number from one term to the next Such sequences are popular as the geometric sequence This topic will explain the geometric sequences and geometric sequence formula with examples.
Geo sequence formula. Sum of the First n Terms of a Geometric Sequence If a sequence is geometric there are ways to find the sum of the first n terms, denoted S n, without actually adding all of the terms To find the sum of the first S n terms of a geometric sequence use the formula S n = a 1 (1 − r n) 1 − r, r ≠ 1,. 3 Determine the eighth term in the sequence 43. Geometric Series Online Calculator Online calculator to calculate the sum of the terms in a geometric sequence If A1, , , An, is a geometric sequence with common ratio r, this calculator calculates the sum Sn given by Sn = A1 An = a1 (1r n )/ (1r) and the nth term an = a1 rn 1.
Finite Geometric Series To find the sum of a finite geometric series, use the formula, S n = a 1 ( 1 − r n) 1 − r, r ≠ 1 , where n is the number of terms, a 1 is the first term and r is the common ratio Example 3 Find the sum of the first 8 terms of the geometric series if a 1 = 1 and r = 2 S 8 = 1 ( 1 − 2 8) 1 − 2 = 255. Given the recursive formula for a geometric sequence find the common ratio, the first five terms, and the explicit formula 11) a n = a n − 1 ⋅ 2 a 1 = 2 Common Ratio r = 2 First Five Terms 2, 4, 8, 16 , 32 Explicit a n = 2 ⋅ 2n − 1 12) a n = a n − 1 ⋅ −3 a 1 = −3 Common Ratio r = −3 First Five Terms −3, 9, −27 , 81 , −243. − − − −n − − − − So the sum of the first n terms of sequence is ;.
Sequence((2, k), k, 1, 3, 05) creates a list of points whose ycoordinates range from 1 to 3 with an increment of 05 {(2, 1), (2, 15), (2, 2), (2, 25), (2, 3)} Sequence(x^k, k, 1, 10, 2) creates the list { x, x³, x⁵, x⁷, x⁹ }. Build a regular SEQUENCE formula and warp it in the ROMAN function For example =ROMAN(SEQUENCE(B1, B2, , B4)) Where B1 is the number of rows, B2 is the number of columns, is the start number and B4 is the step Generate an increasing or decreasing sequence of random numbers. Identify the ratio of the geometric sequence and find the sum of the first eight terms of the sequence 5, 15, 45, 135, 405, 2 A ball is dropped from a height of 10 feet.
Free Geometric Sequences calculator Find indices, sums and common ratio of a geometric sequence stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie Policy. The first term is a = 250 Dividing pairs of terms, I get 1 0 0 ÷ 2 5 0 = 2 5 100 \div 250 = \frac {2} {5} 100÷250 = 52 4 0 ÷ 1 0 0 = 2 5 40 \div 100 = \frac {2} {5} 40 ÷100 = 52 and so forth, so the terms being added form a geometric sequence with common ratio. Day 2 Geo Sequences 3 Using an = 2an1, find the 1st term in the sequence if a4 = 32 Determine if the sequence is arithmetic, geometric, or neither, if possible write the formula for the nth term.
Example 4 generating a formula for nth term of a geo sequence The second term in a geometric sequence is 4 and the fifth term is 32 1 Determine a formula for the nth term of this sequence 2 Which term has a value of 1 024?. Taking a pair of numbers from the sequence and dividing them produces the common ratio, providing the numbers chosen border each other 6 / 3 = 2 12 / 6 = 2 24 / 12 = 2 Etc Geometric Sequence Formulas 1 Terms Formula a n = a 1 (r n1) 2 Sum Formula S n = a 1 (1 r n) / (1 r) Where a n is the nth term of the sequence, a 1 is the. Sn = a(1 − rn) 1 − r Now given you know r n and the sum you find a by re arranging.
Aₙ = 1 * 2ⁿ⁻¹, where n is the position of said term in the sequence A common way to write a geometric progression is to explicitly write down the first terms This allows you to calculate any other number in the sequence;. To find the sum of a finite geometric series, use the formula, S n = a 1 (1 − r n) 1 − r, r ≠ 1, where n is the number of terms, a 1 is the first term and r is the common ratio Example 3. Sequence Traslate poly1,n u, n, 0, 5 Sequence Traslatec,n u, n, 0, 5 Where poly1 is a square of side 2 units, c is a circle and its centre is the centre of poly1, and u is the vector (2,0) If we try to change properties, such as colour or filling, it changes the properties of all the elements of the list.
A geometric sequence is a sequence where each term is found by multiplying or dividing the same value from one term to the next We call this value "common ratio" Looking at 2, 4, 8, 16, 32, 64,, carefully helps us to make the following observation As you can see, each term is found by multiplying 2, a common ratio to the previous term. Cubic Sequences, how to find the formula for the nth term, using the difference methodCubic sequences of numbers are characterized by the fact that the thi. Sequence and Series > A finite geometric sequence is a list of numbers (terms) with an ending;.
This algebra video tutorial provides a basic introduction into geometric series and geometric sequences It explains how to calculate the common ratio of a. Sequence Traslate poly1,n u, n, 0, 5 Sequence Traslatec,n u, n, 0, 5 Where poly1 is a square of side 2 units, c is a circle and its centre is the centre of poly1, and u is the vector (2,0) If we try to change properties, such as colour or filling, it changes the properties of all the elements of the list. The formula for calculating the geometric mean is where n is number of numbers and X1 are the numbers from the first to the nth An alternative way to write the formula is (X1 x X2 x )^1/n This formula is used in our calculator A geometric approach to explain the formula is through rectangles and squares.
Common ratio ‘r’ = 2 a= 1 (first term of the sequence) a n = a 1 r (n – 1) a 5 = 1 × 2 (5 – 1) a 5 = 1 × 2 (4) a 5 = 1 × 16 a 5 = 16 The 5 th term for this sequence is 16 Individual Parts Of The nth Term Formula Of Geometric Sequence The formula for the nth term of a geometric sequence is Where a n nth term of the sequence a 1. For our example, we would write the series as 1, 2, 4, 8,. The Formula of Arithmetic Sequence If you wish to find any term (also known as the {n^{th}} term) in the arithmetic sequence, the arithmetic sequence formula should help you to do so The critical step is to be able to identify or extract known values from the problem that will eventually be substituted into the formula itself.
A3 = 3 (–2) 3 = (3) (–8) = –24 So this is a geometric series with common ratio r = –2 (I can also tell that this must be a geometric series because of the form given for each term as the index increases, each term will be multiplied by an additional factor of –2 ) The first term of the sequence is a = –6. The terms of a geometric series are also the terms of a generalized Fibonacci sequence (F n = F n1 F n2 but without requiring F 0 = 0 and F 1 = 1) when a geometric series common ratio r satisfies the constraint 1 r = r 2, which according to the quadratic formula is when the common ratio r equals the golden ratio (ie, common ratio r = (1. Geometric sequences can be represented by the general formula aarar 2 ar 3 where r is the fixed ratio while exponential function has the following formula f(x)= b x where b is base value and x is a real number.
The step/common ratio is r;. Identify the Sequence, , This is a geometric sequence since there is a common ratio between each term In this case, multiplying the previous term in the sequence by gives the next term In other words, Geometric Sequence This is the form of a geometric sequence Substitute in the values of and. Day 2 Geo Sequences 3 Using an = 2an1, find the 1st term in the sequence if a4 = 32 Determine if the sequence is arithmetic, geometric, or neither, if possible write the formula for the nth term.
Question 1 If 4,7,10,13,16,19,22is a sequence, Find Common difference;. Divide each term by the previous term to determine whether a common ratio exists 2 1 = 2 4 2 = 2 8 4 = 2 16 8 = 2 2 1 = 2 4 2 = 2 8 4 = 2 16 8 = 2 The sequence is geometric because there is a common ratio The common ratio is 2 12 48 = 1 4 4 12 = 1 3 2 4 = 1 2 12 48 = 1 4 4 12 = 1 3 2 4 = 1 2. An = a1rn−1 a n = a 1 r n − 1 Let’s take a look at the sequence {18, 36, 72, 144, 2, } { 18 , 36 , 72 , 144 , 2 , } This is a geometric sequence with a common ratio of 2 and an exponential function with a base of 2 An explicit formula for this sequence is an =18 ⋅2n−1 a n = 18 ⋅ 2 n − 1.
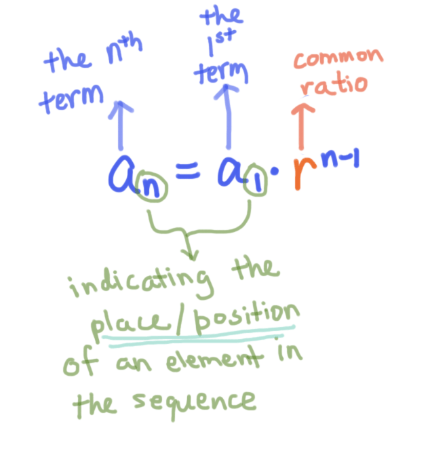
Formulas The formula for finding $n^{th}$ term of a geometric progression is $\color{blue}{a_n = a_1 \cdot r^{n1}}$, where $\color{blue}{a_1}$ is the first term and $\color{blue}{r}$ is the common ratio The formulas for the sum of first $n$ numbers are $\color{blue}{S_n = a_1 \frac{1r^n}{1r}}$. Since arithmetic and geometric sequences are so nice and regular, they have formulas For arithmetic sequences, the common difference is d, and the first term a 1 is often referred to simply as "a" Since we get the next term by adding the common difference, the value of a 2 is just. In an arithmetic progression the difference between one number and the next is always the same 1 4 7 10 13 is an example of an arithmetic progression that starts with 1 and increases by 3 for each position in the sequence This sequence can be described using the linear formula a n = 3n − 2 In a geometric progression the quotient between one number and the next is always the same 2 4.
A geometric seriesis the sum of the terms in a geometric sequence If the sequence has a definite number of terms, the simple formula for the sum is Formula 3 This form of the formula is used when the number of terms ( n), the first term ( a1), and the common ratio ( r) are known Another formula for the sum of a geometric sequence is. In mathematics, a geometric progression (sequence) (also inaccurately known as a geometric series) is a sequence of numbers such that the quotient of any two successive members of the sequence is a constant called the common ratio of the sequence The geometric progression can be written as ar0=a, ar1=ar, ar2, ar3,. Finding Common Ratios The yearly salary values described form a geometric sequence because they change by a constant factor each year Each term of a geometric sequence increases or decreases by a constant factor called the common ratioThe sequence below is an example of a geometric sequence because each term increases by a constant factor of 6.
For example, the sequence 2, 10, 50, 250, 1250, 6250, , , is a geometric progression with the common ratio being 5 The formulas applied by this geometric sequence calculator are detailed below while the following conventions are assumed the first number of the geometric progression is a;. The formulas applied by this geometric sequence calculator are detailed below while the following conventions are assumed the first number of the geometric progression is a;. Solution Given sequence is, 4,7,10,13,16,19,22 a) The common difference = 7 – 4 = 3 b) The nth term of the arithmetic sequence is denoted by the term T n and is given by T n = a (n1)d, where “a” is the first term and d, is the common difference.
Geometric Sequences and Series Consider the sequence of numbers 4, 12, 36, 108, Each term, after the first, can be found by multiplying the previous term by 3 This is an example of a geometric sequence A sequence in which each term, after the first, is found by multiplying the previous term by a constant number is called a geometric. The fourth number times 1/2 is the fifth number 2 × 1/2 = 1 Because these sequences behave according to this simple rule of multiplying a constant number to one term to get to another, they are called geometric sequences. The step/common ratio is r;.
An geometric sequence is one which begins with a first term () and where each term is separated by a common ratio () eg ;. Sequence formula mainly refers to either geometric sequence formula or arithmetic sequence formula To recall, all sequences are an ordered list of numbers Example 1,4,7,10 all of these are in a proper sequence That is each subsequent number is increasing by 3. Math Formulas Arithmetic and Geometric Series Notation Number of terms in the series n First term a 1 Nth term a n Sum of the rst n terms S n Di erence between successive terms d Common ratio q Sum to in nity S Arithmetic Series Formulas 1 a n = a 1 (n 1)d 2 a i = a i 1 a i1 2 3 S n = a 1 a n 2 n 4 S n = 2a 1 (n 1)d 2 n Geometric Series Formulas 5 a n = a 1 qn 1 6 a i = p a i 1 a i1.
Let's look at other examples of geometric sequences 6, 12, 24, 48, 96, 4, 6, 9, 135, The first sequence has a common ratio of 2 12/6 = 24/12 = 48/24 = 96/48 = 2 The second sequence. Each term is multiplied by the same amount (called a common ratio) to get the next term in the sequence For example the sequence 5, 10, , 40, 80, 3 ends at 3 Each term is multiplied by 2 to get the next term Note A slightly different form is the geometric series, where terms are added. The nth term to be found in the sequence is a n;.
In order to predict the nth n t h term of a sequence you will need to create a formula For sequence patterns of geometric progressions or geometric sequences (or multiplications) this is worked out by using the formula arn−1 a r n 1 Where a = a = first term r = r = the multiple n = nth n = n t h number. So let's look at the formula for the sum of an infinite geometric sequence But first, let's review the formula for the sum of a finite geometric sequence, which is this formula here Sn is the sum of the nterms a1 is the first term in this sequence r is the common ratio between any two consecutive terms, and n is the number of terms that we're summing. Day 2 Geo Sequences 3 Using an = 2an1, find the 1st term in the sequence if a4 = 32 Determine if the sequence is arithmetic, geometric, or neither, if possible write the formula for the nth term.
The formula for a geometric sequence is a n = a 1 r n 1 where a 1 is the first term and r is the common ratio. A geometric sequence is a sequence derived by multiplying the last term by a constant Geometric progressions have many uses in today's society, such as calculating interest on money in a bank account So if you were wondering how exactly you would work out how much money you'll have in there in a few years, this article will help you find out. A geometric sequence refers to a sequence wherein each of the numbers is the previous number multiplied by a constant value or the common ratio Let’s have an example to illustrate this more clearly For instance, you’re growing root crops Let’s assume that for each root crop you plant, you get root crops during the time of harvest.
A geometric sequence is a sequence where each term is found by multiplying or dividing the same value from one term to the next We call this value "common ratio" Looking at 2, 4, 8, 16, 32, 64,, carefully helps us to make the following observation As you can see, each term is found by multiplying 2, a common ratio to the previous term. The sum of the geometric progression is S Then a n = ar n1 If r ≠ 1 then S = a(1r n/(1r). A geometric sequence is a sequence of numbers where the ratio of consecutive terms is constant This ratio is called the common ratio (r) Sometimes the terms of a geometric sequence get so large that you may need to express the terms in scientific notation rounded to the nearest tenth 2, 6, 18, 54,.
A = 10 (the first term) r = 3 (the "common ratio") The Rule for any term is xn = 10 × 3(n1) So, the 4th term is x 4 = 10 × 3 (41) = 10 × 3 3 = 10 × 27 = 270 And the 10th term is x 10 = 10 × 3 (101) = 10 × 3 9 = 10 × 196 = 1960 A Geometric Sequence can also have smaller and smaller values. This geometric sequence has a common ratio of 3, meaning that we multiply each term by 3 in order to get the next term in the sequence The recursive formula for a geometric sequence is written in the form For our particular sequence, since the common ratio (r) is 3, we would write. The following geometric sequence calculator will help you determine the nth term and the sum of the first n terms of an geometric sequence Guidelines to use the calculator If you select a n , n is the nth term of the sequence.
Math Formulas Arithmetic and Geometric Series Notation Number of terms in the series n First term a 1 Nth term a n Sum of the rst n terms S n Di erence between successive terms d Common ratio q Sum to in nity S Arithmetic Series Formulas 1 a n = a 1 (n 1)d 2 a i = a i 1 a i1 2 3 S n = a 1 a n 2 n 4 S n = 2a 1 (n 1)d 2 n. A n is the nth term of the sequence When writing the general expression for a geometric sequence, you will not actually find a value for this It will be part of your formula much in the same way x’s and y’s are part of algebraic equations.

3 Convergent Series Compound Interest Ppt Download

Mathwords Infinite Geometric Series

Geometric Progression Series And Sums An Introduction To Solving Common Geometric Series Problems
Geo Sequence Formula のギャラリー
Geometric Sequences And Sums

Find The Number Of Terms In A Geometric Sequence Youtube

How To Find The Nth Term Of A Geometric Mean Sequence Algebra 2 Honors Mathgotserved Ratio U9l4 Youtube

Geometric Sequences And Sums

Geometric Progression Wikipedia
Geometric Sequences Precalculus I
Geometric Sequences And Series Mathbitsnotebook Ccss Math

Math Exercises Math Problems Geometric Sequence

The Sum Of An Infinite Geometric Series Is 15 And The Sum Of The Squares Of The Terms Is 45 Find The Series Mathematics Topperlearning Com N1s3kmrr

Using Explicit Formulas Of Geometric Sequences Video Khan Academy

Geometric Sequences

Geometric Progression Wikipedia
Unit 1 Sequences And Series Positively Mathematics

Geometric Sequences And Series Examples Solutions Videos
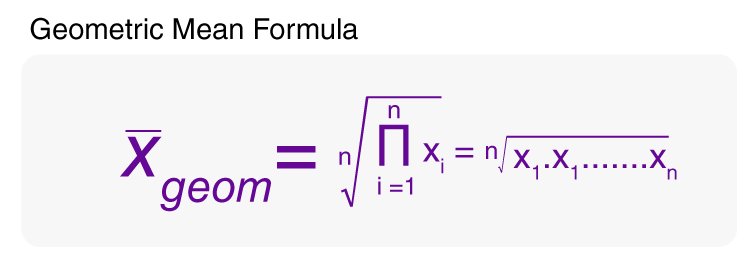
Geometric Mean Formula With Explanation And Solved Examples

Exam Questions Geometric Series Examsolutions
Q Tbn And9gcqffis1upddkpgmhbaephqqndb81qb8kjxgjvpxsz0d9cxxghw5 Xqtpy1vn358m3c54ml3hswrtyqgatcbpper1x2gkbkxlgbpna0xqx75 Usqp Cau Ec

Alternate Formula For Sum Of Finite Geometric Series Second Form Mathlibra

Geometric Sequence Video Lessons Examples And Solutions
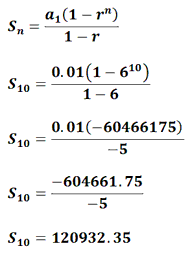
Geometric Sequences And Series
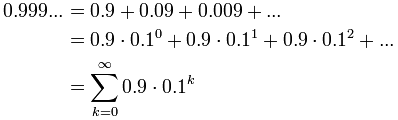
Geometric Sequences And Sums

Arithmetic And Geometric Series And Summation Formulas Geogebra

Using Recursive Formulas Of Geometric Sequences Video Khan Academy

How Do You Determine If A Sequence Is Arithmetic Or Geometric Virtual Nerd
2 2 Arithmetic And Geometric Sequences Mathematics Libretexts

Using Recursive Formulas Of Geometric Sequences Video Khan Academy

70 Arithmetic And Geometric Sequences Ideas Geometric Sequences Arithmetic Teaching Math

Solved Determine Whether Each Sequence Is Arithmetic Geo Chegg Com

Geometric Sequences And Series Examples Solutions Videos

Geometric Progression Series And Sums An Introduction To Solving Common Geometric Series Problems
Q Tbn And9gcq12lclkcsloswedubksl Cjjxcixtrtejuynm7x H0m0wgldq3r1xc Iz2ep45zlmcd6rugxa3itqgbg5npcczrfy6ukb4rwgjyk91oyhh Usqp Cau Ec

Math Exercises Math Problems Geometric Sequence
Geometric Sequence Explicit Formula Youtube

2 3 Sequence Series

Arithmetic Geometric Sequences Ppt Download

Homework Questions Geometric Sequences In A Geometric Sequence The Ratio Between Consecutive Terms Is Constant This Ratio Is Called The Common Ratio Ppt Download

Explicit Formulas For Geometric Sequences College Algebra

Geometric Sequences Video Lessons Examples And Solutions

1 4 3 Sum Of The First N Terms Of A Geometric Progression Spm Additional Mathematics
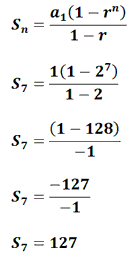
Geometric Sequences And Series

Geometric Series Wikipedia

Geometric Sequence Video Lessons Examples And Solutions
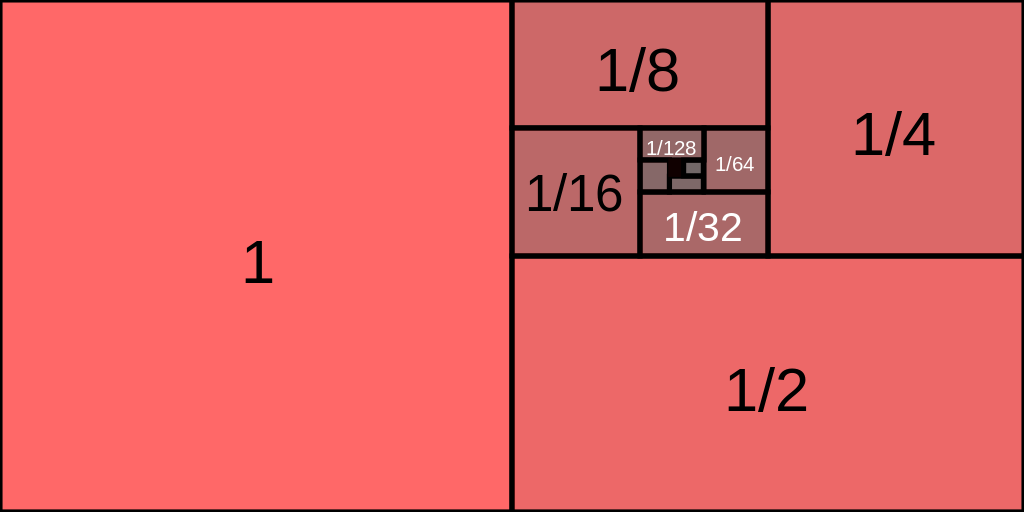
Geometric Sequence Calculator

Geometric Sequence Calculator Symbolab

Geometric Sequence Equation Formula Tessshebaylo

Understand The Formula For Infinite Geometric Series Video Lesson Transcript Study Com

Recursive Equation For Geometric Sequences Youtube

Recursive Formulas For Geometric Sequences Practice Khan Academy

Recursive Formulas For Geometric Sequences Practice Khan Academy

Geometric Sequences Sequences And Series Siyavula

Ap Calculus Review Geometric Series Magoosh Blog High School

Geometric Sequences And Sums
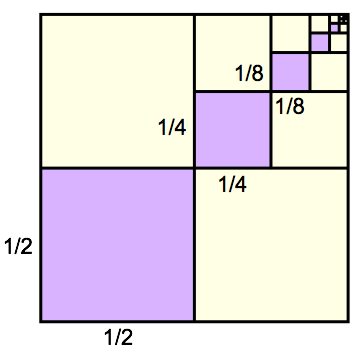
Geometric Sequences And Series Boundless Algebra

Solved 1 Point Local Setseries Geometric Infinite Geo Chegg Com

What Is The Explicit Formula For The Nth Term In A Geometric Sequence Virtual Nerd
Www Lakeview2167 Com Cms Lib02 Mn Centricity Domain 123 8th arithmetic and geometric sequences Pdf

Geometric Sequence Worksheets

Geometric Series Ck 12 Foundation

Algebra 2 Worksheets Sequences And Series Worksheets

Geometric Sequence Worksheets

Geometric Sequence Calculator

Geometric Progression Geeksforgeeks
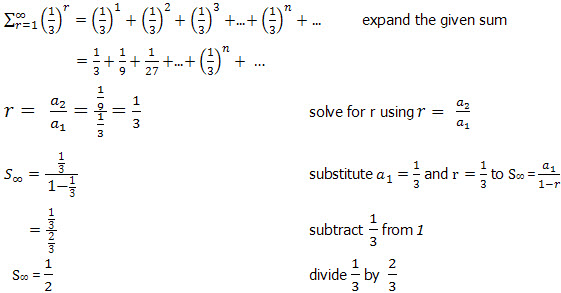
Geometric Progression Series And Sums An Introduction To Solving Common Geometric Series Problems

34 Arithmetic And Geometric Sequences Worksheet Worksheet Resource Plans

How Do I Find The General Formula Of This Non Geometric Arithmetic Sequence Mathematics Stack Exchange

Geometric Mean Video How To Find Formula Definition Tutors Com

Derivation Of The Formula For The Sum Of A Geometric Series Youtube

How To Find N In A Geometric Series

Geometric Sequences Ck 12 Foundation
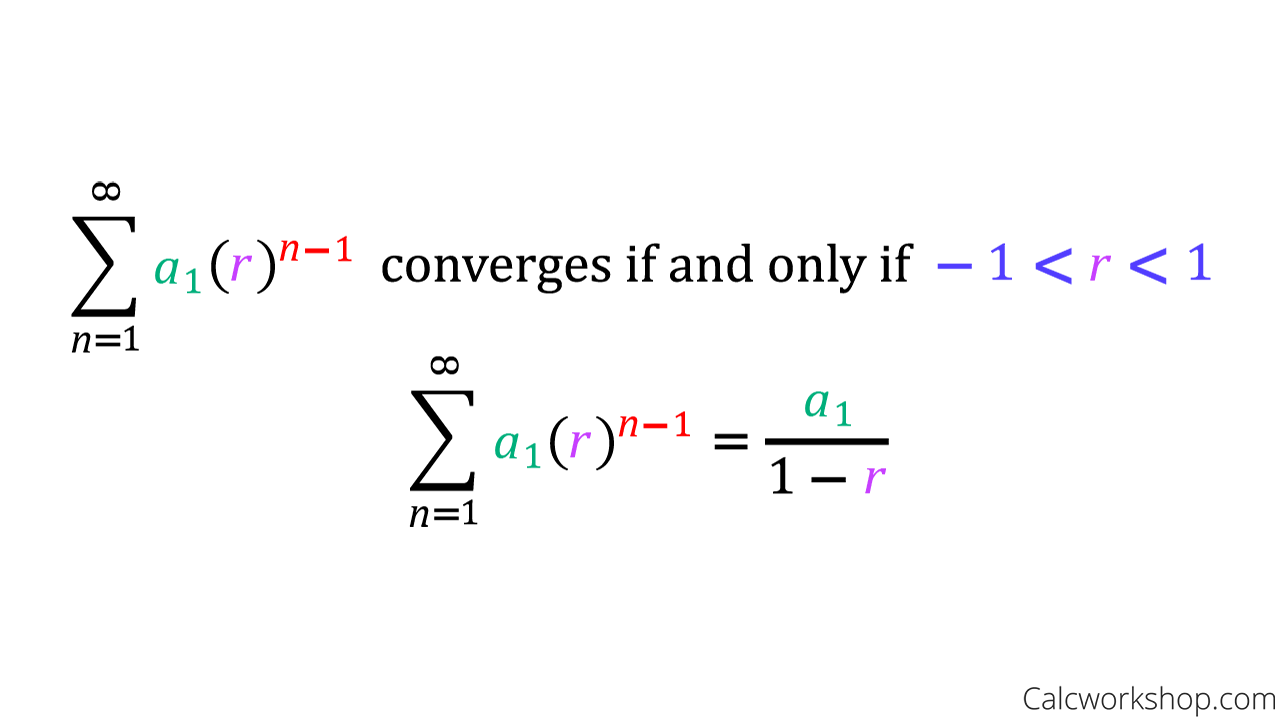
Geometric Series

Use Geometric Sequence Formulas Practice Khan Academy

Recursive And Explicit Formulas For Geometric Sequences Expii

Chapter One Algebra Ii Flashcards Quizlet
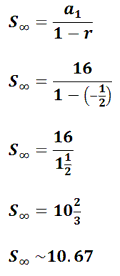
Geometric Sequences And Series
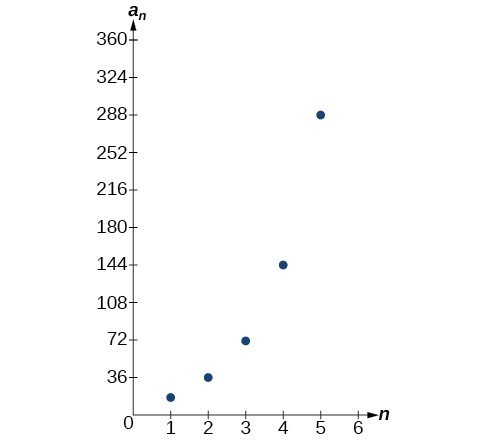
Explicit Formulas For Geometric Sequences College Algebra
Http Www Lancasterschools Org Cms Lib Ny Centricity Domain 250 Algebra ccls Alg unit 7 Alg u7 teacher notes day 4 Pdf
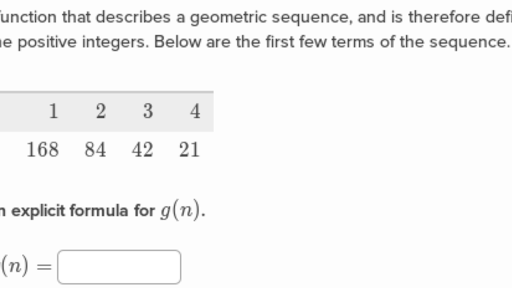
Explicit Formulas For Geometric Sequences Practice Khan Academy
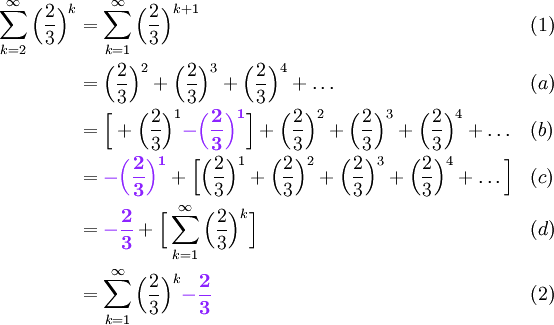
A Geometric Series Problem With Shifting Indicies The Infinite Series Module

Geometric Series Test To Figure Out Convergence Krista King Math Online Math Tutor

Geometric Sequences And Series Further Maths U3 4

Geometric Sequences And Series Further Maths U3 4

Patterns Sequences And Series

Geometric Sequences And Geometric Means

Geometric Sequence Problem Find X Youtube

Geometric Progression Geeksforgeeks

113a Geometric Sequences Explicit Formula
Geometric Series Wikipedia

How Do You Write A Rule For A Geometric Sequence Virtual Nerd

Geometric Sequences Sequences And Series Siyavula

Lesson 6 7 Geometric Sequences Faribault Public Schools Isd 656

Geometric Sequences And Series Further Maths U3 4
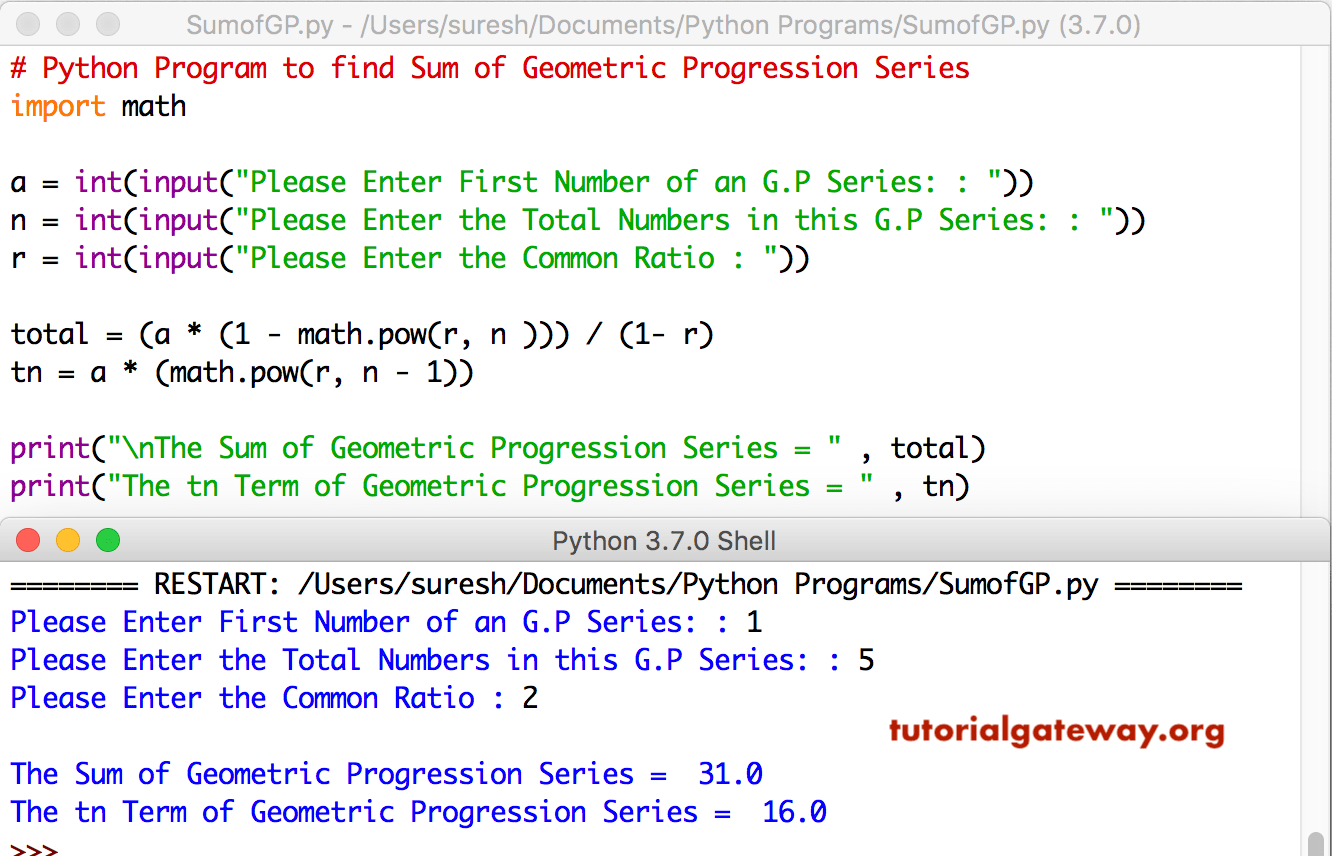
Python Program To Find Sum Of Geometric Progression Series

Geometric Progression Series And Sums An Introduction To Solving Common Geometric Series Problems

How And Why To Use The General Term Of A Geometric Sequence Video Lesson Transcript Study Com

Geometric Series Applications Examples Solutions Videos Worksheets Activities
Q Tbn And9gcqffis1upddkpgmhbaephqqndb81qb8kjxgjvpxsz0d9cxxghw5 Xqtpy1vn358m3c54ml3hswrtyqgatcbpper1x2gkbkxlgbpna0xqx75 Usqp Cau Ec
Q Tbn And9gctpnxkg0fcnks6c Sdlqyugepk3kgc Lfo8cfmtlogph5rgatpcgziqffq2k6g07hnawuejjsvyvwmlwlese3vxkn31amzxfji3agzish Usqp Cau Ec

Understand The Formula For Infinite Geometric Series Video Lesson Transcript Study Com
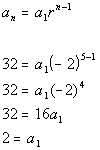
Wtamu Math Tutorials And Help
Geometric Sequences And Series Mathbitsnotebook Ccss Math
Recursive And Explicit Formulas For Geometric Sequences Expii



